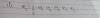🔄 System of Particles & Rotational Motion Notes – JEE/NEET 2025 Preparation

Cracking JEE/NEET Physics? This post gives you a comprehensive overview of Chapter 7 – System of Particles & Rotational Motion, complete with essential definitions, formulas, diagrams, and solved examples. Perfect for mastering concepts like center of mass, torque, moment of inertia, angular momentum, and energy in rotational systems.

 

Internal Forces :-

• All forces exerted by various particles of the system on one another are called internal forces. 

• Internal forces between any two particles are mutual that is internal forces between a pair of particles are equal and opposite hence such forces cancel out in pairs.

External Forces :-

• Forces excited on a given system by the agencies outside the system is called external forces

Expression for centre of mass for descrete mass system:-

Center of mass

Negative mass concept

  

Motion of center of mass:-

Example of motion of center of mass :-

From the motion of centre of mass , it should be clearly understood when there is no external force , centre of mass either have constant velocity or at rest also the momentum of centre of mass is same or conserved .

 Analogues :-

Analogues

Moment of force :-

When an external force acting on a body has a tendency to rotate the body about a fixed point or fixed axis, it is said to exert a torque on the body .
Moment force = force × perpendicular distance

Analogues 

Angular momentum:-

Angular momentum 

Relation between angular momentum and torque :-

Relation between angular momentum and torque 

Center of mass in continuous mass system:-

C.O.M of uniform mass distribution 

Types of mass distribution:-

Mass distribution 

1. Center of mass of uniform rod :-

C.O.M of uniform rod

2. Center of mass of semicircular Ring :-

C.O.M of semicircular Ring

3. Center of Mass of Hollow hemisphere:-

C.O.M of Hollow Hemisphere 

4. Center of mass of semicircular disc :-

C.O.M of semi-circular disc

5. Center of mass of Triangular Lamina :

C.O.M of Triangular Lamina 

Center of mass trick :-

C.O.M trick

Moment of Intertia (I) 

A quantity that measures the inertia of the rotational motion of the body is called rotational inertia or moment of inertia .

Inertia (I) depends upon:-

(i) position of the axis of rotation
(ii) orientation of the axis of rotation
(iii) shape of the body
(iv) size of the body
(v) distribution of the mass of the body about the axis of rotation

Moment of Inertia 

1. Moment of Inertia of ring about an axis which is passes through center of mass and it is perpendicular to plane of ring 

M.O.I of Ring 

2. Moment of Inertia of a uniform rod along the axis passes through its center of mass  

M.O.I of Rod

3. Moment of Inertia of disc about an axis passing through its center of mass and perpendicular to plane of disc 

M.O.I of disc

4. Moment of inertia of completely hollow cylinder about an axis 

M.O.I of Hollow cylinder 

Moment of Inertia of Hollow sphere, solid sphere, hollow cone, solid cone respectively

M.O.I of Hollow sphere, solid sphere, hollow cone and solid cone

Perpendicular axis theorem:

Statement :-

The moment of inertia about any of its axes which are perpendicular to the plane is equal to the sum of the moment of inertia about any two perpendicular axes in the plane of the body which intersect the first axis in the plane.

Perpendicular axis theorem 

Applications:- 

Application of perpendicular axis theorem 

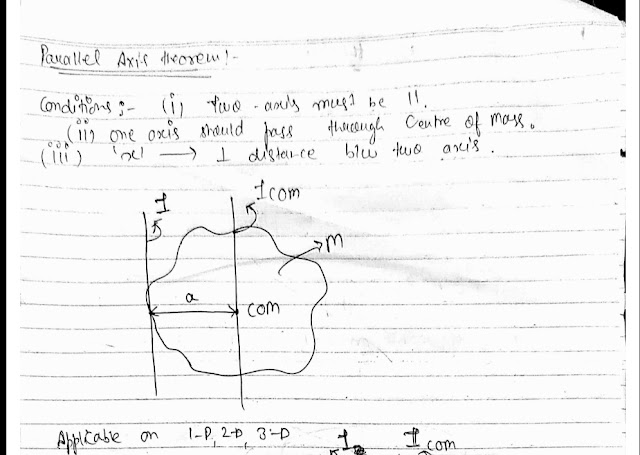
Parallel axis theorem 

Statement:-

The moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of the moment of inertia of the body about the axis passing through the centre and the product of the mass of the body times the square of the distance of between the two axes.

Applications:-

Parallel axis theorem on uniform rod

Parallel axis theorem on disc and Ring

Parallel axis theorem on solid sphere

Equilibrium

A body in general can execute translation as well as rotational motions.

Equilibrium 

Couple

A pair of equal and opposite forces with different line of action one said to form a couple .

Example:- 

When we open the lid of a bottle by turning it our fingers applied couple on the lid .

Radius of gyration (K) 

Statement:-

It is the perpendicular distance from the axis of rotation and from centre of mass, where the moment of inertia is same at that axis of center of mass and the point perpendicular distance to that .

Radius of gyration 

Rolling Motion 

Rolling Motion 

Derive an expression for acceleration of solid sphere rolling down incline plane with angle of inflation theta 

Rolling Motion on an incline plane

✅ Final Tip: Regularly revise these core formulas and solve at least one problem daily to build strong intuition in rotational dynamics.
👍 Found this guide helpful? Bookmark, share, and comment with any doubts or questions!

📥 Download PDF: System of Particles & Rotational Motion Notes (PDF)